How to Model Multi-Stage Terminal Values
As James Bond theme-song singer Shirley Bassey once crooned, “Cash Flows are forever, they are all I need to please me…. I’ve no fear that they might desert me”. Ok, maybe not quite.
For those who use Discounted Cash Flow (“DCF”) for valuation, you have probably heard the common criticism: “the result is too sensitive to terminal value assumptions because so much of the value lies in the terminal period”. This is certainly a valid point – in many models, the present value of the terminal value can make up 75% or more of the total value. Another common complaint is that DCF terminal growth rates are unreasonable. Even if you use a multiple to arrive at the terminal value, it still implies a perpetual growth rate for the free cash flows – and this growth rate should be reasonable relative to overall economic growth.
So one might argue that a terminal growth rate of say 3% or more is too high because it implies the company will grow at a rate that exceeds the overall economy in perpetuity – i.e. eventually that company will become the economy and take over the world! (If that happened, we’d want it to be a chocolate bar manufacturer by the way).
One way to make more sense of terminal growth rates is to split the terminal period into two or more streams of cash flows (i.e. a multi-stage terminal value), as follows:
Part 1: Assume cash flows after the model period grow for a certain number of years at a constant growth rate as a growing annuity – for example, in a 5-year model you might assume that the company’s cash flows grow at 6% during years 6 to 10.
The formula for a growing annuity is as follows:
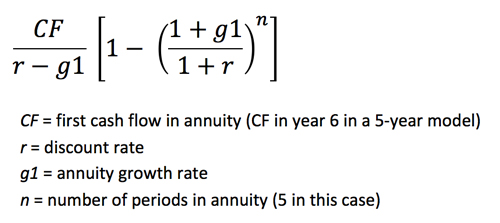
Remember that the PV of this annuity will still need to be discounted back to the valuation date.
Part 2: Calculate the remainder of the terminal value the way you normally would, say using the perpetuity growth (i.e. Gordon Growth) method
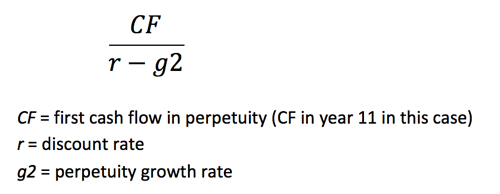
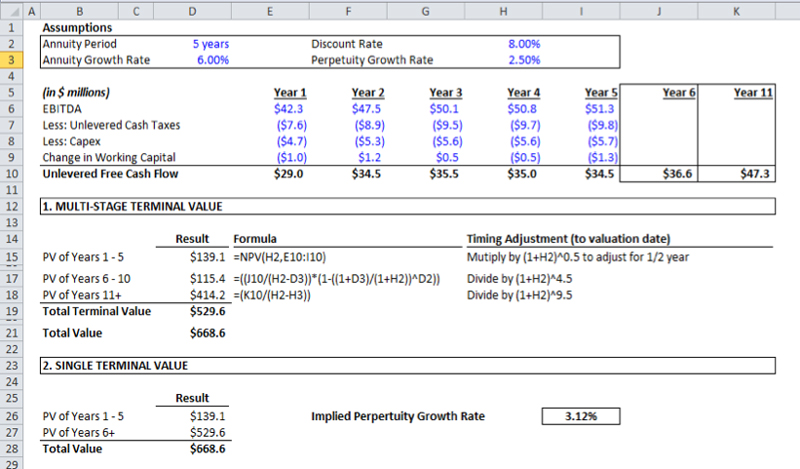
An Example:
In the example below, we show the DCF two ways and derive the same answer:
- Multi-stage terminal value: Here we assume an annuity for years 6-10 growing at 6% and we then assume that cash flows grow in perpetuity at 2.5%.
- Single terminal value: To get the same answer as in the multi-stage version, we solve for the terminal growth rate required to equal the present value of the two-part terminal value.
Note that the implied perpetual growth rate in the single terminal value model is around 3.1%. This might seem a little high in isolation, but when broken into the assumptions contained in the multi-stage model, it seems more reasonable.
Of course, you can employ the same logic to break the terminal value into more than two parts by having multiple annuities and then a perpetuity.
The other thing to consider is that unlike diamonds, cash flows don’t really go out forever when you calculate a terminal value using a perpetuity. That’s because the present value of very distant cash flows is negligible. If you take a cash flow of $10 million in year 100 and discount it back by 100 years at 10%, the present value of that cash flow is literally $726. That represents 0.01% of the original cash flow value of $10 million.
Good luck in your pursuit of cash flows (or diamonds) that go on forever.
Let us know if you have any questions about this technique.